ZIP
Circles: Angles and Arcs
Objectives
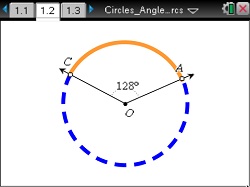
- Students will know the definitions of and identify central angles, major and minor arcs, intercepted arcs, and inscribed angles of a circle.
- Students will determine and apply the following relationships: · Two inscribed angles intercepting the same arc have the same measure. · An inscribed angle measure of 90° results in the endpoints of the intercepted arc lying on a diameter. · The measure of an angle inscribed in a circle is half the measure of the central angle that intercepts the same arc.
Vocabulary
- Central angle
- Inscribed angle
- Major arc
- Minor arc
- Intercepted arc
About this lesson
This lesson involves manipulating endpoints of an arc, manipulating an inscribed angle, and manipulating the vertex of an angle intercepting an arc. As a result students will:
- Use visualization to understand the definitions of central angle, intercepted arc, and minor and major arcs.
- Infer that the sum of the measures of minor and major arcs is 360°, that two inscribed angles intercepting the same arc have the same measure, and that the inscribed angle has half the measure of the central angle that intercepts the same arc.
- Deduce that the opposite angles of a quadrilateral inscribed in a circle are supplementary.